Numerical Notation in Africa
urn:nbn:de:0009-10-35535
Zusammenfassung
Die in Afrika verwendeten Systeme numerischer Notationen, aus dem alten Ägypten bis in die moderne Zeit, werden analysiert und in Tabellen dargestellt. Die Grundlagen der numerischen Dar-stellung werden kurz beschrieben.
Abstract
Systems of numerical notations used in Africa from the Ancient Egypt till modern time are reviewed. Tables of symbols are presented. Basic principles of numeral representation are briefly described.
Résumé
Les systèmes de notations numériques utilisées en Afrique de l'Egypte ancienne jusqu'à l'époque moderne sont passés en revue. Tables de symboles sont présentés. Les principes de base de la représentation en chiffres sont brièvement décrits.
<1>
Mathematics has accompanied humans from deep in antiquity. Simple means of mathematical notation appeared in the late Paleolithic age and were presumably connected with calendar or akin records. As Africa is believed to be a cradle of humanity, it is not surprising that the most ancient presently known mathematical artifact was found there. It is the so called Lemombo bone discovered in the 1970s in the Lemombo Mountains between the South Africa and Swaziland and dated to approximately 35,000 BC. (Bogoshi et al. 1987). Another object to mention here is the Ishango bone from an area near Lake Edward (Nile headwaters, border between Uganda and Congo), see, for instance, Yellen (1998).
Such systems of notation predate writing by many thousand years. However, at a certain stage of the development of a society, economical needs require a more complicated numerical notation, which usually becomes associated with systems of writing. Discussion on mathematics in pre-colonial Africa beyond writing can be found in a paper by Huylebrouck (2006). Typological analysis of numerical notation systems in different regions of the world was made by Zhang & Norman (1995) and Chrisomalis (2004; 2010).
Further in this paper we review more than three dozens of numerical notation systems used in Africa since antiquity till the modern age. More information is given for less known systems, while other are described briefly. For ancient numeric notation, the main source is Cajori (1928). An extensive overview of different numerical notation systems with respect to their typology was recently made by Chrisomalis (2010). In the present work, additional information is given about numerical notation in some recently invented African scripts. Due to space considerations, most systems are discussed concisely, with the details on their functioning available in cited sources.
The African continent is known as a homeland for one of the most ancient writing systems, Egyptian hieroglyphs, and the Egyptian numerals will be the first subject of this work. We then proceed to other non-positional systems, paying special attention to the alphabetic notation of numerals in Section II. Positional notations are briefly described in Section III. Short discussion concludes the paper.
<2>
The history of Egyptian hieroglyphic notation dates back to the mid-fourth millennium BC (Cajori 1928: 11; Chrisomalis 2010: 35). A cursive writing form known as Hieratic was used for recording documents on papyrus. In the first millennium BC another, more cursive and abbreviated, form of the Egyptian script appeared. It is known as Demotic.
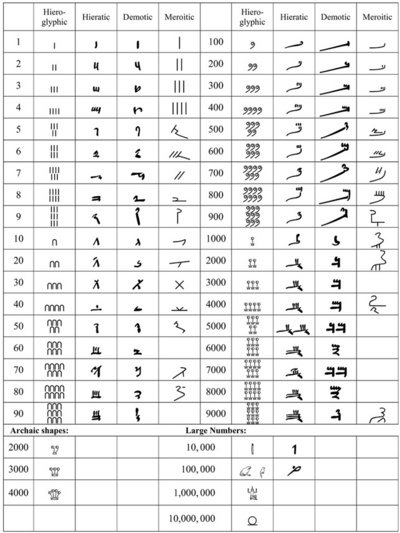
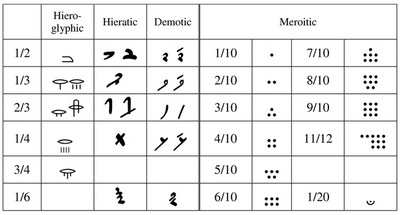
The comparison of numerical signs in these three forms of the Egyptian writing is presented in Table 1.1. The fourth column shown there is the Meroitic script, a writing system which evolved in the ancient kingdom of Meroë (presently Northern Sudan) in the second half of the first millennium BC.
<3>
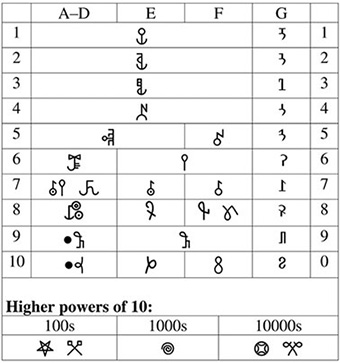
In Egyptian hieroglyphic script, the following signs were used to denote powers of ten: a vertical stroke for 1, a hook for 10, a rope for 100, the lotus plant for 1,000, the pointing finger for 10,000, a tadpole for 100,000 (Cajori 1928: 12 gives either a bird shape or a burbot for this number). One million is the cosmic deity Ḥḥ (Cajori 1928: 12; reading adapted from Chrisomalis 2010: 37). The ten million sign seems to be some abstract shape.
<4>
The signs were repeated up to nine times to denote the respective numbers. They were arranged in rows, each having no more than four signs, and with a larger group placed above the smaller one (note signs for 5, 7, 50, 70, etc.).
The digits were written according to the direction of writing, with higher ones preceding lower ones. In hieroglyphic inscriptions, both right-to-left and left-to-right directionality can be found, with human and animal figures facing toward the beginning of the line and thus helping to determine how the text should be read. Vertical arrangement of symbols is also attested. In Hieratic and Demotic scripts, the right-to-left order was already fixed. Hence, the number 232,613 in the hieroglyphic right-to-left inscription would appear as:
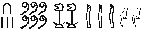 (2 × 100,000 + 3 × 10,000 + 2 × 1,000 + 6 × 100 + 10 + 3).
(2 × 100,000 + 3 × 10,000 + 2 × 1,000 + 6 × 100 + 10 + 3).
Sometimes, a multiplicative notation was used. Namely, if the symbols of lower power value are placed before the higher one, this means multiplication:
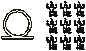 would denote 9 million multiplied by 10 million.
would denote 9 million multiplied by 10 million.
|
Table 1.1: Egyptian and Meroitic numerals. |
|
|
|
For hieroglyphic writing, the shape found in right-to-left inscription is shown. When the direction of text was left-to-right, the signs had to be mirrored. Signs for 1 and ten sometimes occur in a horizontal position (– and ⊂) when writing calendar dates (Chrisomalis 2010: 36). |
<5>
Special system of fraction notation was developed in Egypt as well. Except for a symbol for one half, there were special symbols for 1/3, 2/3, and 3/4 constructed similarly to a regular manner. This regular notation of fraction was used to write so called unit fractions with the numerator equal to unity. Other fractions were decomposed as a sum of unit fractions. This was indicated by a lenticular symbol placed above the number symbol corresponding to the denominator (cf. 1/4 and the right symbol for 1/3 in Table 1.2).
<6>
In the Hieratic and Demotic scripts the notation of fractions became quite cursive often not allowing for a simple symbol decomposition.
In Hieratic script a dot was placed over a numeral to represent unit fractions. For instance, the number 5 5/7 is decomposed into unit fractions as:
|
5 5/7 |
= |
5 10/14 |
= |
5 + 1/2 + 1/7 + 1/14 |
and in the so called Rhind Mathematical Papyrus (or Ahmes Papyrus) is written as follows (Cajori 1928: 15):
|
|
Note that in cursive writing shapes of symbols varied substantially depending on the time, territory, and obviously a scribe.
<7>
Meroitic fractions are thought to represent numbers n/10 with n ranging from 1 to 9. There are some evidences of the n/12 notation (Griffith 1916; 1925). A special mark denoted one half of 1/10, i.e. 1/20, see Table 1.2.
|
Table 1.2: Egyptian and Meroitic fractions |
|
|
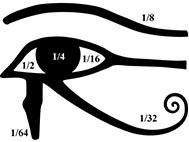
There was an interesting system of fraction notation to represent 1/2, 1/4, 1/8, 1/16, etc. of the hekat, an Egyptian volume unit of about 4.8 liter. It is based on the symbol known as the Eye of Horus (Peet 1923; Kavett & Kavett 1975):
|
|
Thus, the brow denoted 1/8, the pupil corresponded to 1/4, the left part of the eye was 1/2, etc.
<8>
Various numerical notations were used in Africa during the first millennium BC in Phoenician and Greek colonies. These include in particular Greek Attic or Herodianic notation, Phoenician or Punic and Aramaic Elephantine notation, Cyrenaic notation, and certainly Roman numerals.
<9>
The Acrophonic principle was used to represent numerals in the Attic notation, see Table 1.3. An archaic shape of Π (with a shorter right leg) was typically applied to form numerals 50, 500, etc. Numerals were further composed of the basic forms given in the table and written left-to-right with the highest value placed leftmost (Chrisomalis 2010: 99).
|
Table 1.3: Attic numerals |
|
|
<10>
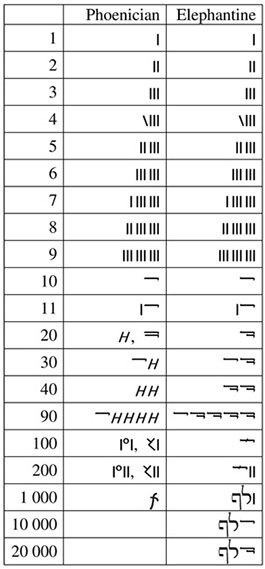
Some of the numerical notation systems of Levant, namely Phoenician and Aramaic, certainly reached Africa and were used in the colonies, in particular in Elephantine, an island in the Nile River, now a part of Aswan. These systems were quite similar structurally, see Table 1.4. For numbers 1–9 vertical strokes were repeated the required number of times, grouped by three. The last stroke was occasionally slanted when single. Special signs were used for 10, 20, 100, and 1,000 (Gandz 1932/33). In the Elephantine notation, the latter () is composed of two last letters of the <1>
<11>
Aramaic root ‘-l-p’ for ‘thousand’. For higher numbers, the multiplicative principle was applied, namely, the number of hundreds or thousands was placed before the sign for 100 or 1,000. The numerals were written according to the direction of the script, right-to-left, with highest value placed first, i.e., rightmost (Chrisomalis 2010: Chap. 3).
|
Table 1.4: Phoenician and Elephantine numerals |
|
|
<12>
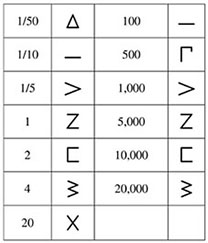
A special notation of monetary values was discovered in the Greek colony of Cyrene (Κυρήνη, modern Shahhat, Arabic شحات, in north-eastern Libya). The same sign was applied to values differing in 5,000 times (obviously, an approximate price of a commodity was easily identifiable). It might be linked to the relation between currency units of that period, namely 1 talent = 5,000 drachmas (Chrisomalis 2010: 100–101). The system becomes irregular for lower values (< 1/5), see Table 1.5.
|
Table 1.5: Cyrenaic numerals |
|
|
<13>
Roman numerals certainly were used in Africa in Roman colonies. This notation is probably well known for readers due to its widespread use in modern time. For the history and detailed description of the Roman numerical notation system one can consult various sources, just cf. Cajori (1928) or Chrisomalis (2010).
<14>
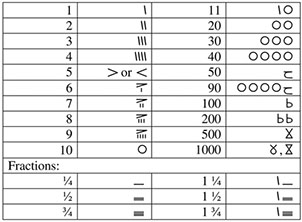
By jumping over almost two millennia in time and moving to the western direction, one would observe quite simple numerical notation among Berbers still in use in the 19th century (Hanoteau 1860; Vycichl 1952). In this system numerals are composed of signs for 1, 5, 10, 50, 100, and 1,000, see Table 1.6. The existence of the symbol for 500 is discussable (Chrisomalis 2010: 320). Numerals are written right-to-left and sometimes stacked vertically, like shown for 6–9. A horizontal bar is used as a 1/4 fraction.
<15>
Curiously, the Berber numerical notation is not associated with the indigenous Tifinagh script. At least, no evidence of such symbols can be observed in pagination or writing dates. Sometimes numerals are written lexically in Tifinagh texts, cf. samples given by Elghamis (2011).
|
Table 1.6: Berber numerals |
|
|
<16>
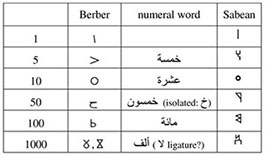
The origins of this numerical notation are not clearly established. The shape of numerals can be acrophonic, see Table 1.7. Note that number words in Berber languages are mostly of Arabic origin (Souag 2007). The applied acrophonic principle might be even related to the South Arabian (or Sabean) numerals (see Table 1.7), were the numerical symbols are just first letters of the respective word in the Sabean script. The symbol for ‘50’ is just a half of that for ‘100’ (Vycichl 1952).
|
Table 1.7: Berber and Sabean numerals |
|
|
<17>
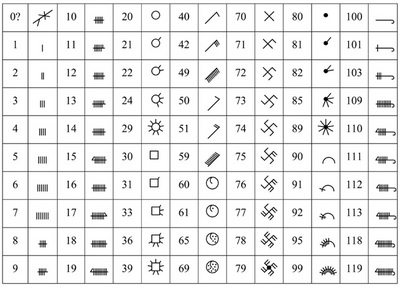
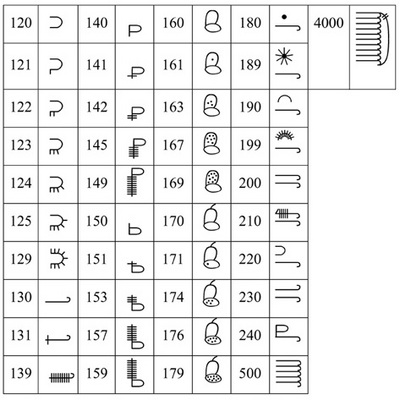
Quite interesting numerical notation was observed within Bambara (Bamana) people of Mali (de Ganay 1950). The system was used for religious purposes and seems not to be associated with any script used for the Bamana language. Neither the origins of this notation nor any peculiarities of its usage are known (Chrisomalis 2010: 318).
The set of symbols in this numerical notation is large. Each decade till 180 has a special mark. Units are marked by the respective number of strokes. Some ideas how the numerals are formed can be grasped from Table 1.8.
It seems that for numbers between 1,000 and 2,000 a different notation principle is used:
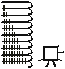 stands for ‘1936’.
stands for ‘1936’.
It is not clear, however, if, e.g., 1,200 would be denoted as
 or
or

The sign for a thousand with an arc to the right denotes 2,000, cf. the value of 4,000 in Table 1.8 (two strokes on the ark give 2 × 2,000). The largest value reported corresponds to a symbol obtained by adding an arc to the ‘thousand’ symbol on the left. This reads as 10 000. So, just hypothetically, the number of 80,000 = 8 × 10,000 would look like the following one having eight strokes:
|
Table 1.8: Bambara numerals |
|
|
|
|
<18>
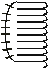
Of non-positional notations, the most developed system emerged within Mende.
The Mende script, or Ki-ka-ku-i from the recitation order, was created in 1917 by Mohamed Turay from Maka in Sierra Leone, near the Liberian border (Tuchscherer 2005). His work was then continued in 1921 by Kisimi Kamara from Barri Chiefdom, who is often credited as script’s inventor (Dalby 1967).
The Mende script was used mainly for private correspondence and recordkeeping up to ca. 1940, when a Roman-based orthography was adopted for Mende. The script is a right-to-left running alphabet.
<19>
The Mende numerical notation is not just a simple substitution of western decimal digits. Separate symbols are used for units 1–9. There are two signs for ten: one being additive to represent numerals 11–19 and another one being multiplicative to form 20–90. For larger numbers (100 onwards) a symbol of the J shape is used with the order of ten denoted by the number of vertical strokes (Tuchscherer 1996: 71–75, Chrisomalis 2010: 323–325), see Table 1.9. One can see in the notation of large numbers the precursor of positional notation.
|
Table 1.9: Mende Numerals |
|
|
<20>
There is an interesting non-positional numeric notation associated with a newly proposed Ndebe Igbo script by Lotanna Ọdunzẹ, a native of Anambra (Nigeria). The script is seen as an alternative to write the Igbo language, primarily the Anambra Igbo (Rovenchak & Glavy 2011: 107–108). Separate signs are used for units and tens, while symbols for numbers above 100 take a number diacritic distinct from the signs for units, see Table 1.10. For instance, the number 186,282 is written as follows:
|
|
The role of the symbol for zero remains unclear.
|
Table 1.10: Ndebe Igbo numerals |
|
|
|
Note: The diacritic placeholder is marked by a dotted circle. |
<21>
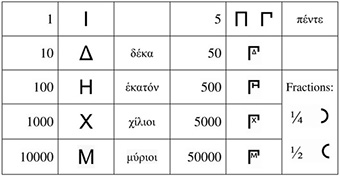
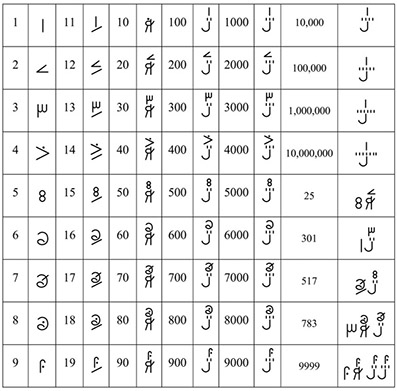
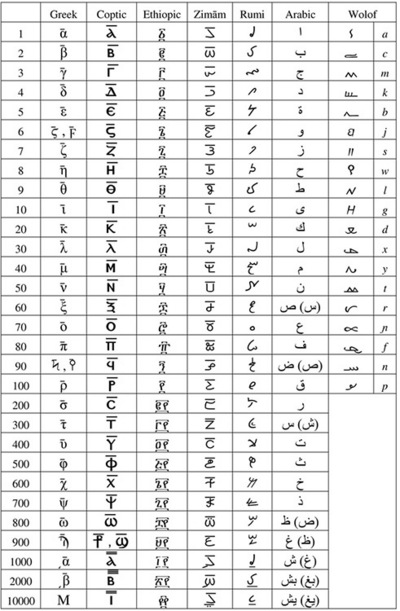
As soon as the order of letters in an alphabet became fixed, this opened a way to use the letters as numeric signs. Notwithstanding the fact that alphabets first emerged among Semitic peoples, first of all Phoenicians, it seems quite reasonable to suggest the Greeks being the inventors of alphabetic numeric notation ca. the sixth century BC (Chrisomalis 2010: 134). This system known as the Ionic or Milesian notation followed the Attic or Herodianic notation described in the previous section. The Greeks used three archaic letters to supplement their 24-letter alphabet expanding its capacity to denote unities, tens, and hundreds fully. Alphabetic numeric notation was borrowed by the Copts together with the alphabet, and also later by some other people, namely, Slavs, Armenians, Goths, etc.
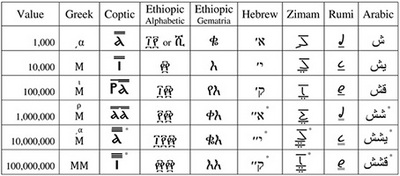
In ancient Greek manuscripts the letters denoting numerals were distinguished from that for words by an overline, while modern practice is to add an acute-like sign on top-right of the numeral letter sequence. The archaic letters supplementing the Greek alphabet are: stigma (ϛ) or digamma (ϝ) for ‘6’, koppa (ϟ or ϙ) for ‘90’, and sampi (ϡ) for ‘900’, see Table 2.1. Thousands are marked by symbols for unities 1–9 preceded by a small stroke placed mostly to the bottom-left. Myriads (10,000s) are marked in a number of ways, in particular by the capital ‘M’ with the number of myriads placed above or before it (see Tables 2.1, 2.2). Another approach was to place a trema (dieresis or umlaut) above the letter for unities (Heath 2003: 18), e.g.
|
|
= |
10,000 |
The numerals were written left to right, with letters for lower digits following that for higher ones, thus σμπ for 248 = 200 + 40 + 8.
<22>
Special symbols were used for fractions 1/2, 2/3, and 3/4 (see Table 2.5), while other unit fractions were written with a stroke on the top-left of the symbol corresponding to the denominator. This approach is however not a unique one and other ways to write fractions are also known (Heath 2003: 20–24).
|
Table 2.1: Alphabetic numerical notation |
|
|
|
Note: Arabic alphabetic numerals are given for the western (Maghreb) system, with the eastern one in parentheses. |
|
Table 2.2: Notation of large numerals in some alphabetic systems. |
|
|
|
Asterisks denote suggested notation not confirmed in the available sources |
The letters of the Coptic alphabet, being a descendant of Greek, were used to write numerals in a similar fashion. Some deviation can be observed in notation of thousands and myriads (Mallon 1907: 76–77), see Table 2.2: symbols
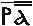 correspond to 100 × 1,000 = 100,000, while
correspond to 100 × 1,000 = 100,000, while
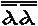 denote 1,000 × 1,000 = 1,000,000, with another order is marked by an additional overline:
denote 1,000 × 1,000 = 1,000,000, with another order is marked by an additional overline:
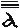 for 10,000,000. It should be noted that, as it was usually for alphabetic systems of numerical notation, large numerals did not have a firmly established representation standard, and for instance Chrisomalis (2010: 136–137 and 148) cites only numerals up to 9,000 written just in the Greek fashion. The Coptic alphabetic numerals were mostly used from the fourth to the tenth centuries AD, but they still remain as a notation system within the Coptic Church.
for 10,000,000. It should be noted that, as it was usually for alphabetic systems of numerical notation, large numerals did not have a firmly established representation standard, and for instance Chrisomalis (2010: 136–137 and 148) cites only numerals up to 9,000 written just in the Greek fashion. The Coptic alphabetic numerals were mostly used from the fourth to the tenth centuries AD, but they still remain as a notation system within the Coptic Church.
<23>
Ethiopic number shapes are also of Greek origin, see Table 2.1. In this system, however, all the signs after ρ (100) are abandoned and larger numbers are formed by a multiplicative approach, with the number of hundreds placed before the sign ፻ for ‘100’. The next new sign was ፼, a ligature of two ፻, denoting 100 × 100 = 10,000. Occasionally, the symbol ሺ shi is used for ‘thousand’, but rather with western numerals, not with the Ethiopic ones. Large numerals can be obtained by the multiplicative principle (http://www.geez.org/Numerals/), see Table 2.2.
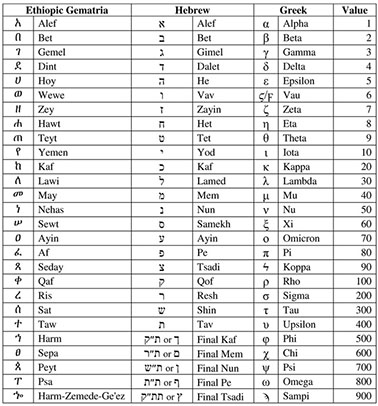
Two types of numerological notation are also associated with the Ethiopic script (http://www.geez.org/Numerals/Numerology.html). One was almost directly copied from Hebrew Gematria, see Table 2.3. Note that values from 500 to 900 did not have a unique sign in the Hebrew system. The sign for 900 in the Ethiopic Gematria system is taken from the additional zemede series of signs for labiovelars, as does the sign for 1,000 (see Table 2.2). The symbol for 10,000 is alef-sadis /’ə/, while all the previously mentioned ones belong to geez series /-ä/.
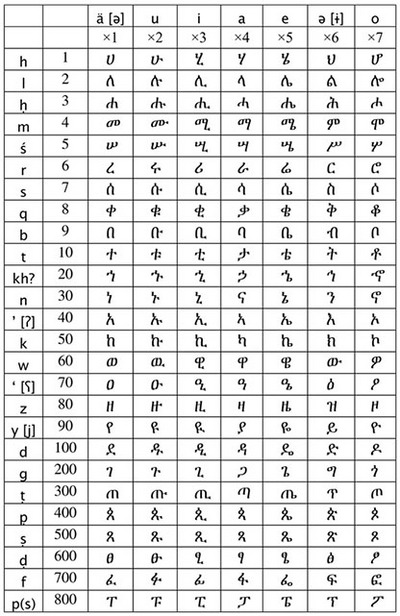
The complete table of the Ethiopic script is used in the Debtera (Halehame) system, see Table 2.4. The first series ending in /-ä/ correspond to numerals 1 to 800, while in subsequent columns these values are multiplied by 2, 3, etc. to 7 for the /-o/ series. Thus the maximum value in this system is 5600. However, it seems that only the numbers from the first series were used in numerological calculations ( http://www.geez.org/Numerals/Numerology.html ).
|
Table 2.3: Ethiopic Gematria compared to Hebrew and Greek alphabetic systems |
|
|
|
For detailed description of Hebrew numerals, see Gandz (1932/33). |
|
Table 2.4: Ethiopic Debtera (Halehame) system |
|
|
<24>
In the tenth century AD an alphabetic system based on the cursive script evolved in Egypt. This system is known as “numerals of the Epakt”, Zimām numerals, or Coptic numerals (Chrisomalis 2010: 149–150). Except for the symbol shapes, the system is similar to Coptic and Greek alphabetic notations described above (see Tables 2.1, 2.2). The numbers were written left to right, with symbols for highest values place on the left. From available descriptions (Sesiano 1989; Goldstein & Pingree 1981) it does not become sufficiently clear how the numerals from ten million were formed. Zimām numerals survived as long as the seventeenth century, being later replaced by the Arabic positional numerals (Chrisomalis 2010: 152).
<25>
Arabic alphabetic notation spread in Africa together with Islam in the seventh century (Cajori 1928; Chrisomalis 2010). In main features, it resembles the Greek principle as the arrangement of letters mostly corresponds to the Greek order and not to that of the Arabic alphabet. The presence of the 28th letter allowed the extension of the notation to thousands in a natural way, see Table 2.1. A simple multiplicative principle is known for the numbers over 1,000 (Cajori 1928: 29). Note that the Arabic alphabetic numerical notation is written the same direction as the script does, i.e. right to left with the highest values placed rightmost.
<26>
Rumi numerals known also as Fez numerals (from the city of Fez or Fes, Arabic فاس, a city in Morocco) were used around this area starting from the sixteenth century AD (Chrisomalis 2010: 171). This notation system originated in Spain among the Arabic Christians of Toledo in 12–13th centuries. The numerals are written right to left. Due to cursive writing, the shapes of symbols vary a lot, some generic ones are shown in Table 2.1. Both shapes and structure of the Rumi numeral notation demonstrate influence from Greek, Coptic, Zimām, and Arabic alphabetic system. For instance, there is no mark for multiplication by 10,000, which is the case in Greek, Coptic, and Zimām systems, but not in the Arabic one, where only multiplication by 1,000 is relevant.
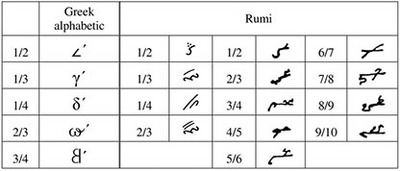
In the Rumi notation special marks were also used for fractions, see Table 2.5 (Lazrek 2006).
|
Table 2.5: Fractions in Greek and Rumi alphabetic numerical notation systems |
|
|
<27>
There is a modern alphabet for Wolof with letters having numerical values. This script is briefly described in the following section. It is not known how the alphabetic numerals are used in this writing system and what are the principles of representing numbers over 100. For the symbol set with phonetic values of letters see two last columns in Table 2.1.
<28>
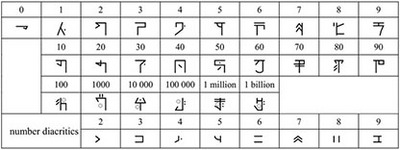
All the systems of positional notations are identical in principle and differ only in three features, namely, digit shapes, the base of the system, and the directionality.
Of all the notation systems we are aware of, all but one are decimal (base-10). The only vigesimal (base-20) system is associated with the Obεri Ɔkaimε script, a writing system invented in the 1930s for the use within an Ibibio Independent Church of the same name, which was active in the Nigerian province of Calabar near Itu on the Western bank of Cross-River. The invention is credited to Michael Ukpɔn and Akpan Udɔfia (Adams 1947; Hau 1961).
|
Table 3.1: Oberi Okaime numerals |
|
|
<29>
The Bamum script was invented by King Ibrahim Njoya (Nʒoya) with a significant contribution of Nji Mama Pekeko and Nji “Adjia” Mborong (Schmitt 1963:109; Tuchscherer 2007). The time of invention is around 1896 (conventionally named “stage A”), and then script underwent six improvement stages (B–G) until 1918. The first version was highly pictographic, while the last one, known as (mfemfe) a-ka-u-ku, is syllabic with some alphabetic features.
It seems that up to the penultimate stage the numerals were written lexically, with special symbols denoting powers of 10, see Table 3.2. Slightly different shapes are cited in different sources for these marks. Two symbols for 10,000 correspond to two Bamum synonyms: nʃüˀ and malɛri (Schmitt 1963: 88). The symbol
|
|
considered as a mark for a unity (Chrisomalis 2010: 322, with reference to Dugast & Jeffreys 1950: 30) is nothing but the Bamum word nʃuɔp ‘and, to that’ used to construct numeral words and placed either after or before unities (Schmitt 1963: 87). Thus:
|
23 |
may be written as |
|
|
1.704 |
may be written as |
|
During stage F, a shift towards positional decimal notation was made. The powers of ten were written by repeating the sign for ‚ten‘ the required number of times. For instance:
|
|
i.e. 2 _ 10 _ 3 |
for |
23 |
|
|
i.e. 1 _ 10 _ 10 _ 2_ 10 |
for |
120 |
|
|
i.e. 1 _ 10 _ 10 _ 10 _ 10 / 4 _ 10 _ 10 _ 10 / 7 _ 10 _ 19 |
for |
14,700 |
|
|
i.e. 2 _ 10 _ 10 _ 10 – 10 _ 10 _ 10 |
for |
2,000,000 |
|
Table 3.2: Bamum numerals |
|
|
When stage G entered into force, the system of numerical notation in Bamum became the decimal positional one, the older symbol for ‘ten’ was used for ‘zero’. The signs for numerals have their own phonetic values and thus can be used to write ordinary words.
<30>
The Bagam script was used for the Mengaka language spoken in the Western Province of Cameroon, Grassfields region, in Bagam, a town located seventy kilometers westward from Foumban. Bagam is the outsiders’ name for these people, while the vernacular one is Eghap (Gordon 2005). The writing system emerged around 1910 (Tuchscherer 1999; 2005; 2007). According to the tradition, the authors are the Bagam king Pufong and his servant Nde Temfong (Tuchscherer 2005). The shapes of many signs show the influence of the Bamum script while those for numbers look differently (Rovenchak 2009). The symbols for 1–10 are listed in Table 3.3. It is quite possible that the notation was not positional but rather similar to that of the stage F of the Bamum script.
<31>
The Vai syllabic script was created in 1820–30s in Liberia by Mɔmɔlu Duwalu Bukεlε, who was probably assisted by five friends (Dalby 1967). The script was used actively in the private sphere, where it, to some extent, still survives to the present. It is believed that this script became a stimulus for the development of several indigenous writing systems, in particular Mende, Loma, and Kpelle.
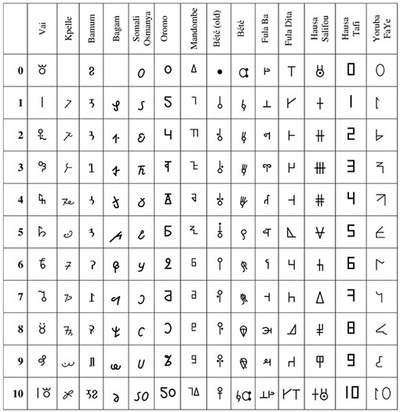
Numerical notation for in Vai is rather marginal and rarely used (Everson et al. 2006). As one can see from Table 3.3, the shape of digits is just a Vai-style adaptation of Western digits.
<32>
The Kpelle syllabic script was created in the 1930s by Gbili, a paramount chief of Sanoyea (Bong County, Liberia) (Dalby 1967). Some evidence of script usage for private records is known even today. The syllabary has some 90 syllables, the most complete set is given in Stone (1990), where in particular the symbols for digits are shown. The latter are rather modern addition. It is not clear how the system of numeral notation functioned. In particular, a separate symbol for ‘10’ suggests that the notation was not purely positional.
<33>
The Somali Osmanya (Cismaaniya) alphabet was developed in 1922 by ‘Isman (Cismaan) Yuusuf Kenadiid, the brother of the Sultan of Obbia (Italian for Somali Hobyo). It had been in use, though not extensively, for about 50 years and partly survived till present as a means for private records (Coulmas 2004: 475). The script is written left to right. Ten decimal digits are original, some influence of the Arabic script is seen in mirrored shapes of ‘7’ and ‘8’, cf. Arabic <۷> and <۸>, respectively (Tosco 2010), see Table 3.3 for the complete list.
The Oromo alphasyllabary was invented in 1956 by Shaykh Bakri Saṗalō (Hayward & Hassan 1981). It is written left to right and is structurally modeled on the Ethiopic script. No information on script’s usage is available. The numerical notation is a simple set of decimal digits (see Table 3.3), unlike the Ethiopic complicated system described above.
<34>
The Mandombe script was created in 1978 by David Wabeladio Payi from Mbanza Ngungu, Bas-Congo (now Kongo Central) Province in the Democratic Republic of the Congo (formerly Zaire). It is used by representatives of the Kimbanguist Church, mainly for Kikongo, Lingala, Tshiluba, and Swahili languages (Pasch 2010; Rovenchak & Glavy 2011: 84–86). Structurally the script is an alphasyllabary. Signs for decimal digits are original (Wabeladio Payi 1996:44–45), see Table 3.3; the shapes of 1–5 are used also as vowel signs for /i, u, e, o, a/, respectively.
<35>
The Bété script was invented in 1952 by Frédéric Bruly Bouabré, an Ivoirean artist. This writing system is a syllabary with over 400 signs of highly pictorial shapes inspired by color pebbles with geometric drawings the inventor found near the Bekora village. A simple system of numerical notation with decimal digits represented by stylized hand with fingers (see Table 3.3) is used in some newer texts written by Bruly Bouabré, in particular for pagination. Older digits are simpler in shape and demonstrate rudimentary quinary system (Chrisomalis 2010), as do in fact the newer ones. The role of the symbol for ‘10’ remains obscure. These signs, however, were not confirmed by the inventor and his family in 2009 (Charles Riley, personal communication 2012). It is probable that the older version of digits was a kind of draft.
<36>
Several alphabets were developed also for the Fula language. One of them was invented before 1964 by Adama Ba from Mali. This “individual” script was used to write his own poetry as well as for correspondence (Dalby 1969). Another alphabet was invented by Oumar Dembele and is known by author’s name Dita. It was created between 1958 and 1966 in Mali. The script is also an individual form of writing (Dalby 1969). The writing direction of both Fula alphabets is left to right. Ten decimal digits accompanying the set of letters in these scripts have deliberately invented shapes, see Table 3.3.
<37>
Several newly suggested orthographies are known for Hausa. Some of them have own shapes for digits. An alphabet called Gobiri is connected to the name of Adaré Salifou. It was created no later than 1998 (Awagana 2008). With a very scarce data available, it can be only mentioned some script’s usage in the areas to the North of Maradi in Niger. The writing direction is left to right. Digits are shown in Table 3.3. Another script called Tafi was suggested by Musa D. Abdullahi, a Nigerian from Katsina, aimed as a writing system for major Nigerian languages: Hausa, Igbo, and Yorùbá (Abdullahi 2005). The script is written left to right. All the signs have simple shapes and digits are very similar to the western ones, see Table 3.3.
An alphabet for Yorùbá called FaYé was invented in 2007 by Remi-Niyi Alaran from Nigeria. This script is a kind of an individual writing system. Ten decimal digits are associated with this left-to-right running alphabet; their shapes given in Table 3.3 (Rovenchak & Glavy 2011: 104).
|
Table 3.3: Decimal numerals in modern African left-to-right running scripts |
|
|
<38>
The evolution of modern digits is extensively studied in literature. In view of this, the present subsection contains only brief account on the history of this issue.
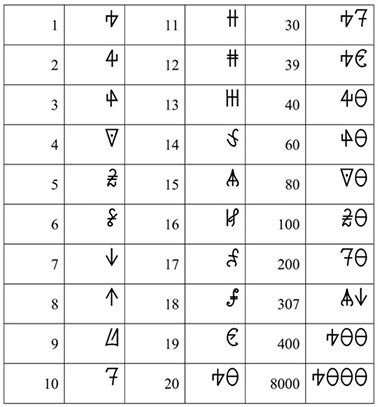
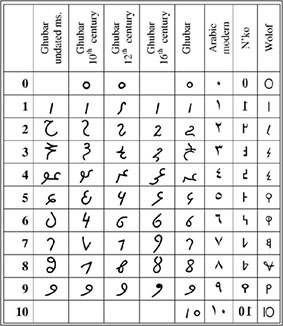
The shapes of modern Western decimal digits are rooted in the so-called Ghubar numerals, first attested in the 9th century in manuscripts from Maghreb (Gandz 1931; (Chrisomalis 2010: 217). The term ghubār (Arabic غبار) ‘dust’ reflects the medium typically used for the calculations with these numerals, i.e., a kind of abacus. The evolution of Ghubar digits is presented in Table 3.4 (adapted from Tropfke 1930).
Among eastern Arabs, different shapes of numerals were used, of which the modern Arabic numerals proper (those associated with the Arabic script) are descendants, see Table 3.4.
Two more African scripts with the right-to-left direction of writing are known to have special signs for decimal digits. Another right-to-left running script, namely the Mende syllabary, was mentioned in Section I because of its indigenous system of numerical notation.
<39>
The Wolof script called Garay was created in 1961 by Assane Faye from Senegal. It is a right-to-left running alphabet. The script is little used; there exist some textbooks, folktales and even maps produced in the Garay alphabet (handwritten). Special symbols for decimal digits are shown in Table 3.4 (Dalby 1969; Coulmas 2004; Rovenchak & Glavy 2011: 56–57).
<40>
The Nko (N’ko) alphabet is the most successful orthographic innovation in modern Africa. The script was invented in 1947–49 by Sòlóomana (Souleymane) Kántɛ, a Guinean scholar and enlightener, and was intended as a writing for Manding (Màndén) group of the Mande family (Niger-Congo languages) of West Africa; /nko/ means ‘I say’ in the languages of this group (Dalby 1969). Nko is used mainly for the Guinean Maninka (Maninka Mori). Beyond Guinea, the alphabet gained some popularity among the Manding speakers in Liberia, Mali, Cotê d’Ivoire, and also within Manding diaspora (mostly in Nigeria and Egypt).
Decimal number digits associated with the Nko alphabet are shown in Table 3.4.
A curious feature of numeric notation in right-to-left scripts is that the order of digits is almost always the same as in left-to-right running scripts, i.e., the least-significant digits are placed to the right. The only known exception is found in the Nko alphabet, where the direction of writing is also transferred onto the direction of number representation, with the least significant digit placed to the left, thus the highest one is written first:
|
Table 3.4: Historical Ghubar numerals and decimal numerals in modern African right-to-left running scripts |
|
|
<41>
In the paper, about forty systems of numerical notation used in Africa in different times were briefly reviewed. Almost all of them are based on ten. This can be seen even in non-positional systems, as new shapes were used for unities, tens, hundreds, etc. in the Egyptian numerals, alphabetic systems also follow this scheme assigning new value of 20, not 11, to a letter after 10, etc.
In most cases a numerical notation system is associated with some script, and respective languages or groups of languages are not that homogeneous. Yet Johnston (1919) noted that in Bantu and semi-Bantu (Bantoid in modern terminology) languages numerals are essentially decimal, cf. the Bamum script. On the other hand, a crucial role of “five” and “twenty” (and to a much lesser extent that of “ten”) is typical for the Mande languages of West Africa (cf. Vai, Kpelle, but especially Mende numerals). The peculiarities of the numeral words, however, do not have much relation to the systems of numerical notations: decimal systems are absolutely predominant. In the numerical notation associated with modern scripts this reflects the processes of globalization. And indeed, not every newly suggested writing system brings a set of numerical signs (cf. Rovenchak & Glavy 2011: 94–107).
References
Abdullahi, Musa D. 2005
A study of writing and development of Tafi, a new Nigerian writing. Fahimta Publishing Co., Katsima. This book was once available at http://uk.msnusers.com/tafiwriting
Adams, R. F. G. 1947
'Obεri Ɔkaimε: A new African language and script.' In: Africa: Journal of the International African Institute 17,1:24–34
Awagana, Ari 2008
'Die Hausa-Schrift.' In: Kootz, Anja and Pasch, Helma (eds.), 5000 Jahre Schrift in Afrika, Universitäts- und Stadtbibliothek Köln, pp.123–126
Bogoshi, Jonas, Kevin Naidoo and John Webb 1987
'The oldest mathematical artefact.' In: The Mathematical Gazette 71,458:294
Cajori, Florian 1928
A history of mathematical notations. Vol. 1: Notations in elementary mathematics. London: The Open Court Company Publishers
Chrisomalis, Stephen 2004
'A cognitive typology of numerical notation.' Cambridge Archeology Journal 14,1:37–52
Chrisomalis, Stephen 2010
Numerical Notation: A Comparative History. Cambridge University Press
Coulmas, Florian 2004
The Blackwell Encyclopedia of Writing Systems. Blackwell Publishing
Dalby, David 1967
'A survey of the indigenous scripts of Liberia and Sierra Leone: Vai, Mende, Loma, Kpelle and Bassa.' African Language Studies 8:1–51
Dalby, David 1969
'Further indigenous scripts of West Africa: Manding, Wolof and Fula alphabets and Yoruba 'holy' writing.' African Language Studies 10:161–181
Dugast, Idelette et M. David W. Jeffreys 1950
L'Écriture des Bamum: sa naissance, son évolution, sa valeur phonétique, son utilisation. Paris: Le Charles Louis
de Ganay, S. 1950
'Graphies bambara des nombres.' Journal des Africanistes 20,2:295–305
Elghamis, Ramada 2011
Le tifinagh au Niger contemporain : étude sur l'écriture indigène des Touaregs. Leiden.
Everson, Michael, Mohamed Nyei, Charles Riley, and Tombekai Sherman 2006
Proposal for addition of Vai characters to the UCS. Available from: http://www.dkuug.dk/jtc1/sc2/wg2/docs/n3081.pdf (01.12.2012)
Gandz, Solomon 1931
'The origin of the Ghubar Numerals.' Isis 16,2:393–424
Gandz, Solomon 1932/33
'Hebrew Numerals.' Proceedings of the American Academy for Jewish Research 4:53–112
Goldstein, Bernard R. and David Pingree 1981
'More Horoscopes from the Cairo Geniza.' Proceedings of the American Philosophical Society 125,3:155–189.
Gordon, Raymond G., Jr. 2005
Ethnologue: Languages of the World. Fifteenth edition. Dallas, Tex.: SIL International, http://www.ethnologue.com ((01.12.2012)
Griffith, F. Ll. 1916
'Meroitic Studies.' The Journal of Egyptian Archaeology 3,1:22–30
Griffith, F. Ll. 1925
'Meroitic Studies V.' The Journal of Egyptian Archaeology 11,3/4:218–224
Hanoteau, Adolphe 1860
'Lettre addressée à M. Reinaud par M. Hanoteau (…) au sujet de la notice qui se trouve ci-devant, p. 107 et suiv.’ [M. Reinaud "Sur le système primitif de la numération chez la race berbère"].' Journal Asiatique, 16:264–271
Hau, Kathleen 1961
'Obєri Ɔkaimє script, text, and counting system.' Bulletin del’IFAN, 23,1–2:291–308
Hayward, R. J. and Mohammed Hassan 1981
'The Oromo orthography of Shaykh Bakri Saṗalō.' Bulletin of the School of Oriental and African Studies 44,3:550–566
Heath, Thomas L. 2003
A Manual of Greek Mathematics. Courier Dover Publications
Huylebrouck, Dirk 2006
'Mathematics in (central) Africa before colonization.' Anthropologica et Præhistorica 117:135–162
Johnston, Harry Hamilton 1919
A comparative study of the Bantu and Semi-Bantu languages. Oxford: Clarendon Press
Kavett, Hyman and Phyllis F. Kavett 1975
'The eye of Horus is upon you. 'The Mathematics Teacher 68(5):390–394
Lazrek, Azzeddine 2006
Rumi Numeral System Symbols, Additional characters proposed to Unicode. Available from: http://std.dkuug.dk/jtc1/sc2/wg2/docs/n3087-1.pdf (DATE).
Mallon, Alexis 1907
Grammaire copte avec bibliographie, Chrestomathie et vocabulaire, Betrouth: Imprimerie Catholique
Pasch, Helma 2010
'Mandombe.' In: Anja Kootz and Helma Pasch, (eds.), 5000 Jahre Schrift in Afrika. Special issue of Afrikanistik online, http://www.afrikanistik-online.de/archiv/2010/2724/.
Peet, T. Eric 1923
'Arithmetic in the Middle Kingdom.' The Journal of Egyptian Archaeology, 9,1/2:91–95
Rovenchak, Andrij 2009
'Towards the decipherment of the Bagam script.' Afrikanistik online, http://www.afrikanistik-online.de/archiv/2009/1912/
Rovenchak, Andrij and Jason Glavy 2011
African writing systems of the modern age: the Sub-Saharan region. New Haven–Buena Park–New Rochelle–London–Lviv–Abidjan: Athinkra LLC.
Schmitt, Alfred 1963
Die Bamum-Schrift: 3 Vols. Wiesbaden: Otto Harrassowitz
Sesiano, Jacques 1989
'Koptisches Zahlensystem und (griechisch-)koptische Multiplikationstafeln nach einem arabischen Bericht.' Centaurus, 32:53–65
Souag, Laamen 2007
'The typology of number borrowing in Berber.' In: CamLing 2007, pp.237–244.
Stone, Ruth M. 1990
'Ingenious Invention: The Indigenous Kpelle Script in the Late Twentieth Century.' In: Liberian Studies Journal, 15(2):135–144.
Tosco, Mauro 2010
' Somali writings.' In: Anja Kootz and Helma Pasch, (eds.), 5000 Jahre Schrift in Afrika. Special issue of Afrikanistik online, http://www.afrikanistik-online.de/archiv/2010/2723/.
Tropfke, Johannes 1930
Geschichte der Elementar-Mathematik: In systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter. Dritte, verbesserte und vermehrte Auflage. Vol 1. Berlin and Leipzig: Walter de Gruyter.
Tuchscherer, Konrad 1996
The Kikakui (Mende) syllabary and number writing system: Descriptive, historical and ethnographic accounts of a West African tradition of writing. Ph.D. thesis, University of London
Tuchscherer, Konrad 1999
'The Lost Script of the Bagam.' African Affairs 98,390:55-77
Tuchscherer, Konrad 2005
'History of writing in Africa.' In: Apiah, Kwame Anthony and Henry Louis Gates, Jr. (eds.) Africana: The Encyclopedia of the African and African American Experience. 2nd edition, pp.476–480. New York: Oxford University Press
Tuchscherer, Konrad 2007
'Recording, communicating and making visible: A history of writing and systems of graphic symbolism in Africa.' In: Inscribing Meaning: Writing and Graphic Systems in African Art, pp.37–53. Smithsonian Institution
Vycichl, Werner 1952
'Das Berberische Ziffernsystem von Ghadames und sein Ursprung.' Rivista degli Studi Orientali, 27:81–83
Wabeladio Payi, David 1996
Mandombe Ecriture negro-africaine: Manuel d’apprentissage à l’usage des apprenants. Kinshasa: Editions du C.E.N.A.
Yellen, John E. 1998
'Barbed bone points: Tradition and continuity in Saharan and Sub-Saharan Africa.' In: The African Archaeological Review, 15(3):173–198
Zhang, Jiajie and Norman Donald A. 1995
'A representational analysis of numeration systems.' Cognition 57:271–295
Lizenz
Empfohlene Zitierweise ¶
Rovenchak A (2012). Numerical Notation in Africa. Afrikanistik online, Vol. 2012. (urn:nbn:de:0009-10-35535)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.
Volltext ¶
-
 Volltext als PDF
(
Größe:
3.2 MB
)
Volltext als PDF
(
Größe:
3.2 MB
)
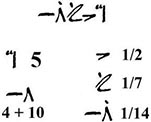
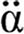

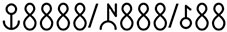
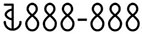

Kommentare ¶
Es liegen noch keine Kommentare vor.
Möchten Sie Stellung zu diesem Artikel nehmen oder haben Sie Ergänzungen?
Kommentar einreichen.